[자료구조] - 트리(1)

Tree

Tree 란?

트리는 연결 리스트와 유사한 데이터 구조이다. 하지만 각 노드가 선형적으로 다른 노드를 가리키는 게 아니라 각 노드가 여러 개의 노드를 가리킨다. 트리는 비선형적 데이터 구조의
한 예이다. 트리 구조는 구조의 계층적 속성을 그래프의 형태로 나타내는 방법이다.

트리 ADT(Abstract Data Type , 추상 데이터형)에서 항목의 순서는 중요하지 않지만,
만일 순서 정보가 필요하다면 연결 리스트나 스택, 큐 등과 같은 선형 데이터 구조를
사용할 수 있다.

Tree 의 용어 설명

root : 부모가 없는 노드. 트리에는 최대 한 개의 뿌리 노드가 있을 수 있다.

edge(간선) : 부모로부터 자식에게 이어지는 연결 선을 뜻한다.

leaf(잎 노드) : 자식이 없는 노드를 잎 노드라고 한다.

siblings(형제 노드) : 같은 부모를 가진 자식들을 형제 노드라고 한다.

조상(ancestor) 노드 : 특정 노드 q에 이르는 경로에 노드 p가 있으면 노드 p를 노드q의
                              조상 노드라고 한다.

자손(descendant) 노드 : 반대로 노드 q는 노드 p의 자손노드가 된다.

Level : 주어진 깊이의 모든 노드의 집합을 그 트리의 레벨이라고 한다. (root 는 Level 0)

노드의 깊이 : root 로부터 그 노드까지의 경로의 길이이다.

노드의 높이 : 해당 노드로부터 가장 깊은 노드까지의 경로
               ※ 노드가 단 한개만 존재한다면 트리의 높이는 0이다. 즉 0부터 시작한다.

노드의 크기 : 자기 자신을 포함하여 그 노드가 가진 자손의 수

이진 트리

- 각 노드가 자식이 없거나, 한개 혹은 2개의 자식을 가질 때 이진 트리라고 한다.

빈 트리 역시 유효한 이진 트리이다. 이진 트리는 root와 왼쪽 부속 트리, 오른쪽 부속 트리

라고 불리는 두 개의 분리된 이진 트리로 구성되어 있다고 볼 수 있다.

이진 트리의 종류

1. 엄격한 이진 트리

   - 모든 노드가 두 개의 자식을 가지거나 자식이 없을 때 엄격한 이진트리 라고 한다.

   

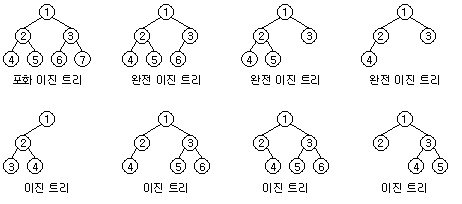
2. 포화 이진 트리

   - 모든 노드가 2개의 자식을 가지고 잎 노드가 같은 레벨에 있을 경우.

 

3. 완전 이진 트리

   - 완전 이진 트리를 정의하기 전에, 이진 트리의 높이가 h라고 할 때, 완전 이진 트리는

     뿌리부터 시작해서 트리 안의 노드 수까지의 완전한 순열을 얻는다.

     탐색할 때 NULL 포인터에게도 숫자를 매겨야 한다. 

     모든 잎 노드가 높이 h나 h-1에 있고 순열에서 빠진 숫자가 없을 때 완전 이진 트리

     라고 한다.

트리의 종류

그럼 트리를 왜 사용 할까?

1. 트리 구조에 저장하면 더 효율적인 자료들이 있기 때문이다.

Ex) 회사나 정부의 조직 구조
     계층적인 데이터의 저장
     인덱스 파일의 생성 ( Ex) B+ Tree )

두번째 포스트에서는 이진 트리의 속성, 이진 탐색 트리에 대해 정리 해보자.


자료 출처 : 다양한 예제로 학습하는 데이터 구조와 알고리즘 for Java

이미지 출처 : 구글..구글..구글..